This is a description of the algorithm for transforming patricia/radix tries into much smaller fractal tries.
Here is a patricia trie that encodes the words Cry, Car, Cart, Dry, Dart, Hart, Hi, Hit, Far, and Fart.
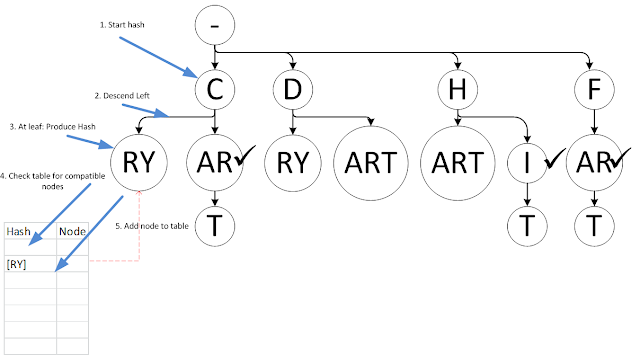
The algorithm runs in a single depth-first traversal. It creates a lookup table, then attempts to calculate a hash for each node in the tree. A node's hash exactly accounts for its entire subtree (it and all its descendants). Here are the first steps illustrated:
Now our table has a hash and reference for one subtree, [RY].
(There's an extra dashed red line here you should ignore.)
Graying out the finished parts and moving along, it continues to try to calculate a hash for C node by descending to its next child (node that while I never show more than two children on these diagrams, thus left/right, tries can have any number of nodes, so it's really 1st child, 2nd child, 3rd child, and so on). This leads it to the T leaf and then it ascends:
Now it has stashed the whole AR:T subtree; while not shown, the hash includes the fact that there is a word termination at the AR node; this prevents non-terminating but otherwise similar subtrees from matching it later. The algorithm continues to complete the C node subtree, then moves on to D node:
Where at this point it encounters the first entire subtree match with a previously encountered subtree. It abandons the "repeat" subtree and moves the parent node's pointer to the tabled subtree, leaving it looking like this:
And we have pruned away a leaf of the trie without sacrificing any knowledge of its structure. Now we'll skip ahead again. We're pruned away an ART node and a T node, and then we have an opportunity to prune an entire subtree:
We find in our table that the AR:T subtree under F exactly matches the AR:T subtree under C, so we immediately redirect. We recurse to the top of the tree and drop the auxiliary table. Then the final trie looks like this:
This trie has the same word structure we started with, and no additional elements in memory. The original patricia trie has 22 letters in 14 nodes. The final trie has 13 letters in 9 nodes. For large tries, the space savings can become quite substantial, sometimes a 3x to 5x difference.
Thursday, February 21, 2013
Tuesday, February 19, 2013
Squeezed tries: fractal compression for words
In this post I explain fractal tries, why I needed to design them, and how they work, with a link to rough prototype code.
Recently I was exploring the new art of culturomics (word crunching, really) and went to load Google word data sets into memory so I could screw around with them. Immediately this presented a problem, because there are a lot of words in Google's word lists. Example: they have 28,771 words that begin with Q. I want to do fancy letter magic, but it's hard to even fit these words into a reasonable amount of memory, much less organize and search them. So I did the obvious and built a trie.
For the sake of quick testing, I used a data set a little smaller than Google's, "Yet Another Word List", with a respectable 264,061 words including 2,457,521 letters. The obvious method of storing these words in memory is like so:
With that arrangement, all letters are represented for all words; it's a simple array of strings of letters. A straightforward, traditional trie arrangement improves on the situation. It uses 586,511 nodes with 1 letter each. Here's a chart that shows how tries store words; on the left is a complete trie for the word "car" alone, while on the right is a complete trie for the words "car, cat, cart, and dart" as in the example above:
In this data structure, all words share as much of their prefixes as they can. A word is indicated in the trie by either ending at the bottom, or having a checkmark/flag to that effect. With such a data structure, you can quickly check for the presence of a word, or reconstruct the whole word list if you choose to.
So there's certainly a savings in terms of total number of letters stored, 76.1%. Unfortunately, each node to node link requires memory, so we actually wind up losing over half a million bytes of RAM compared to just storing them in an array. On the positive side, many different operations such as searching are pretty quick on this data structure. But I needed to fit more words into less memory, so I moved on to another data structure, this time writing a patricia trie, aka radix trie. Here's a chart that shows how patricia tries store the same words used in the previous example:
This chart is not drawn to scale. ;)
In a patricia trie, 'lonely' nodes are minimized. Whenever possible, nodes in the tree that don't need to be separated are collapsed into single nodes with more than one letter in them. This means we store just as many letters as in a regular trie, but we use fewer nodes. In this case, the patricia trie uses the same 586,511 letters but stored in 325,845 nodes, so there is less overhead. We can actually start to see space savings at this point, but not very much.
It seems a little silly to say it this way, but it's truthful and important to note that the purpose of a data structure is to preserve the structure of data. Words are structured in such a way that they frequently share prefixes, so the trie preserves this structure while saving memory space by 'folding together' the beginnings of each word. Each individual word is still represented and recoverable because all the paths through the trie from the root end in a real word.
Words often start the same way (car, carb, carbuncle, carbuncles) but they also often end in predictable ways (preserve, reserve | rested, bested, feasted | least, beast). This highly repetitive structure lends itself to 'folding together' as well. That lead me to the data structure I built next. Since it depends on eliminating self-similar branches all across the trie, I'm calling it a fractal trie (arguably this is an unfractal trie, but whatever):
The first two tries look just like patricia tries, because those word sets do not share suffix structure. With the third fractal trie, we see the trie re-uses an existing node rather than branch out to a new one. The fourth trie shows this continued. But fractal tries can fold over entire suffix trees. For example:
This fractal trie makes extensive re-use of both prefixes and suffixes. The trick, if you like, is in creating such structures in a reasonable amount of time. After consulting with a friend, Ian Bone, I found a method that runs in O(n) linear time. (It's entirely possible that he actually told me how to do this, but I was too dense to realize it at the time, and had to struggle with it for another couple of hours anyway. Thank you Ian.)
When applied to the yawl word list, an implementation of fractal tries creates 65,333 nodes including a total of 145,271 letters. That's a 94% savings in letters stored over the flat string array, and even including the overhead for 65,333 nodes it means a substantial memory space savings when implemented in any reasonable language. (yeah... lots of popular languages are not reasonable in this sense.)
I expect someone else has created data structures like this, and at some point I'll track that down and post an update here with a name and references. In the meantime, I'm happy I designed a data structure that meets my needs. I slammed together a prototype in C#, which due to memory overhead is not a reasonable language for compressing with tries. In C++ it will be much more space efficient by default, there are a variety of optimizations available, and I'll clean up the API.
Subscribe to:
Comments (Atom)