This is a description of the algorithm for transforming patricia/radix tries into much smaller fractal tries.
Here is a patricia trie that encodes the words Cry, Car, Cart, Dry, Dart, Hart, Hi, Hit, Far, and Fart.
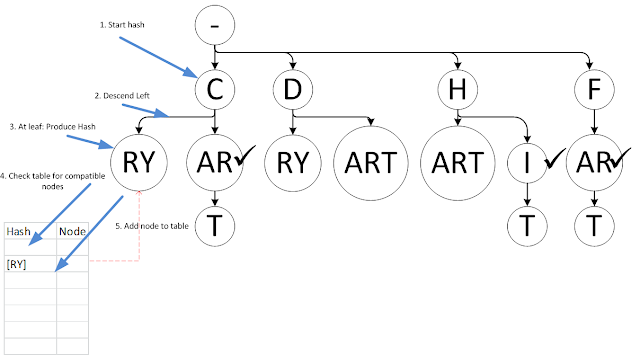
The algorithm runs in a single depth-first traversal. It creates a lookup table, then attempts to calculate a hash for each node in the tree. A node's hash exactly accounts for its entire subtree (it and all its descendants). Here are the first steps illustrated:
Now our table has a hash and reference for one subtree, [RY].
(There's an extra dashed red line here you should ignore.)
Graying out the finished parts and moving along, it continues to try to calculate a hash for C node by descending to its next child (node that while I never show more than two children on these diagrams, thus left/right, tries can have any number of nodes, so it's really 1st child, 2nd child, 3rd child, and so on). This leads it to the T leaf and then it ascends:
Now it has stashed the whole AR:T subtree; while not shown, the hash includes the fact that there is a word termination at the AR node; this prevents non-terminating but otherwise similar subtrees from matching it later. The algorithm continues to complete the C node subtree, then moves on to D node:
Where at this point it encounters the first entire subtree match with a previously encountered subtree. It abandons the "repeat" subtree and moves the parent node's pointer to the tabled subtree, leaving it looking like this:
And we have pruned away a leaf of the trie without sacrificing any knowledge of its structure. Now we'll skip ahead again. We're pruned away an ART node and a T node, and then we have an opportunity to prune an entire subtree:
We find in our table that the AR:T subtree under F exactly matches the AR:T subtree under C, so we immediately redirect. We recurse to the top of the tree and drop the auxiliary table. Then the final trie looks like this:
This trie has the same word structure we started with, and no additional elements in memory. The original patricia trie has 22 letters in 14 nodes. The final trie has 13 letters in 9 nodes. For large tries, the space savings can become quite substantial, sometimes a 3x to 5x difference.
Subscribe to:
Post Comments (Atom)








No comments:
Post a Comment